21.1 INTRODUCTION
There are a growing number of documented scientific therapeutic uses of electricity (Seligman, 1982). In most cases, although the mechanism is not always clearly understood, it appears to arise as a consequence of the depolarization or hyperpolarization of excitable cell membranes resulting from the applied currents. Other mechanisms that appear to be sometimes involved include thermal (heating) and neurohumoral effects. Functional electric stimulation is a very straightforward application for the therapeutic use of electricity. Another area in which electrotherapy may be applied is in the electric stimulation of cardiac tissue, including cardiac pacemakers and cardiac defibrillation. These topics are discussed in the next two chapters.
Functional electric stimulation is a very straightforward application for the therapeutic use of electricity. Another area in which electrotherapy may be applied is in the electric stimulation of cardiac tissue, including cardiac pacemakers and cardiac defibrillation. These topics are discussed in the next two chapters.
 Since the electric stimulation of biological tissues requires the use of electrodes, any practical study should include consideration of electrodes and electrode-tissue interaction. The mechanical properties of electrodes are important particularly with respect to implants whose lifetime is measured in years. Since the flow of electricity from the electrode (where electrons carry the charges) into the tissue (where ions carry the charges) may involve an electrochemical reaction, this area must be carefully studied as well. Consequently, several sections of this chapter are devoted to these electrode characteristics.
Since the electric stimulation of biological tissues requires the use of electrodes, any practical study should include consideration of electrodes and electrode-tissue interaction. The mechanical properties of electrodes are important particularly with respect to implants whose lifetime is measured in years. Since the flow of electricity from the electrode (where electrons carry the charges) into the tissue (where ions carry the charges) may involve an electrochemical reaction, this area must be carefully studied as well. Consequently, several sections of this chapter are devoted to these electrode characteristics.
21.2 SIMULATION OF EXCITATION OF A MYELINATED FIBER
In this and the following section, we consider the behavior of several models of nerve stimulation based on principles of electrophysiology. As the reader will see, these models are fairly simple; this is both an asset (in the mathematical analysis) and a limitation (since we are actually interested in more complex structures). The results are nevertheless important as they provide a starting point toward the elucidation of more realistic models, and as some of the insights gained have wider applicability. In the simplest example of nerve stimulation, a point current source of strength Ia is placed near a uniform myelinated fiber, and both source and nerve are considered to lie in a uniform conducting medium of unlimited extent. In this configuration (as described in Figure 21.1), the source-fiber distance is shown as h, the fiber diameter (i.e., external myelin diameter) do, and axon diameter (internal myelin diameter) di. The internodal length is designated as l, and the ratio of internodal length to fiber diameter is assumed to be a constant (100). This model has been investigated by McNeal (1976), whose paper is closely followed in this presentation.
In the simplest example of nerve stimulation, a point current source of strength Ia is placed near a uniform myelinated fiber, and both source and nerve are considered to lie in a uniform conducting medium of unlimited extent. In this configuration (as described in Figure 21.1), the source-fiber distance is shown as h, the fiber diameter (i.e., external myelin diameter) do, and axon diameter (internal myelin diameter) di. The internodal length is designated as l, and the ratio of internodal length to fiber diameter is assumed to be a constant (100). This model has been investigated by McNeal (1976), whose paper is closely followed in this presentation.
 The electric model corresponding to Figure 21.1 is described in Figure 21.2. In Figure 21.2 it is assumed that transmembrane current is confined solely to the nodal region. More recent experimental work, summarized by Chu and Ritchie (1984), has shown that in the mammalian nerve fiber the potassium channels are found in the internodal axolemma. This appears to introduce quantitative but not qualitative differences in the simpler amphibian (frog) nerve model of Frankenhauser and Huxley (1964), described by Figure 21.2. We shall continue to utilize the latter for its simplicity and qualitatively adequate character.
The electric model corresponding to Figure 21.1 is described in Figure 21.2. In Figure 21.2 it is assumed that transmembrane current is confined solely to the nodal region. More recent experimental work, summarized by Chu and Ritchie (1984), has shown that in the mammalian nerve fiber the potassium channels are found in the internodal axolemma. This appears to introduce quantitative but not qualitative differences in the simpler amphibian (frog) nerve model of Frankenhauser and Huxley (1964), described by Figure 21.2. We shall continue to utilize the latter for its simplicity and qualitatively adequate character.
 Since the node is relatively narrow, the network representing the membrane is essentially described by lumped-parameter elements. These are shown as a parallel RC-structure at all but the central node (node 0). McNeal reasoned that for stimuli up to and including threshold, all nodes (except the central node) respond in a sufficiently linear fashion to require only a passive network representation. Only the central node is described by the Frankenhauser and Huxley (1964) expressions.
Since the node is relatively narrow, the network representing the membrane is essentially described by lumped-parameter elements. These are shown as a parallel RC-structure at all but the central node (node 0). McNeal reasoned that for stimuli up to and including threshold, all nodes (except the central node) respond in a sufficiently linear fashion to require only a passive network representation. Only the central node is described by the Frankenhauser and Huxley (1964) expressions.
 The axial intracellular current path introduces the internodal resistance ri, where
The axial intracellular current path introduces the internodal resistance ri, where
 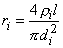 | (21.1) |
| where | ri | = axial intracellular resistance per internodal length [kW/l] |
| ri | = intracellular resistivity [kW·cm] (chosen as 0.1 kW·cm) | |
| l | = internodal length [cm] | |
| di | = axon diameter (internal myelin diameter) [cm] |
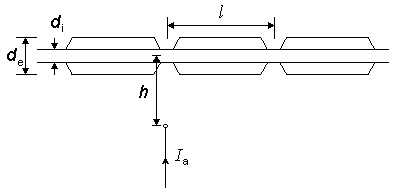
Fig. 21.1 A point current stimulus, Ia, lies at a distance h from a single myelinated nerve fiber. A node of Ranvier is assumed to be aligned with the stimulating monopole. The internodal distance l is related to the outer diameter of the myelin, do (i.e., the fiber diameter, as shown) where l = 100·do.
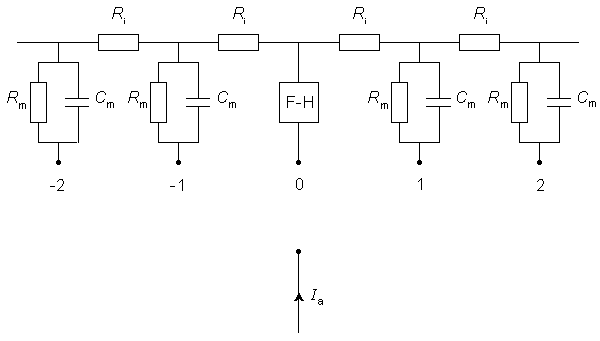
Fig. 21.2 Electric model of a myelinated fiber stimulated by a point current source of strength Ia. The node directly beneath the source is labeled 0 and its membrane is modeled by Frankenhauser-Huxley (F-H) equations. Lateral nodes are assumed to be subthreshold and represented by parallel resistance and capacitance (where Rm, Cm are the total nodal lumped resistance and capacitance per nodal area). The total intracellular internodal resistance is ri.
This formulation, in effect, considers the fiber itself to have little influence on the applied field (i.e., the secondary sources at the fiber surface set up a very weak field compared to Fo arising from Ia and described by Equation 21.2). If one notes the very small extracellular fields generated by nerve impulses propagating on isolated fibers (Plonsey, 1974), then the extracellular potentials from the secondary sources (which are smaller than action potential sources) should certainly be negligible.
The second term of Equation 21.3 expresses the difference of the intracellular axial current entering the nth node (i.e., (Vi,n-1 - Vi,n)/ri) minus that leaving this node (i.e., (Vi,n - Vi,n+1)/ri); this difference has been set equal to the (outward) transmembrane current of the nth node (right hand side of Equation 21.3) which correctly satisfies the conservation of current. Except at n = 0 (the central node governed by the Frankenhauser-Huxley equations) we assume that subthreshold conditions are elsewhere in effect and the ionic current is given by
Using the definition of transmembrane voltage Vn = Vi,n - Vo,n in Equation 21.3 gives
where Equation 21.4 has been substituted for Ii,n. When n = 0, however, one gets
where n is the nodal width, and the ionic currents are found from the Frankenhauser-Huxley equations. The extracellular nodal potentials in Equations 21.5 and 21.6 are found from Equation 21.2, and constitute the forcing function. We assume that the stimulating current is switched on at t = 0 so that Vm,n = 0 for all n at t = 0; the stimulating current is assumed to remain on for a specified time interval. For stimuli that are subthreshold at all nodes (including the central node), Equation 21.5 alone is sufficient to describe the response and may be applied also at n = 0.
 McNeal assumed that the potential on the extracellular side of the nodal membrane was fixed by the stimulating field. Since the latter is a point source (i.e., a monopole), the stimulating (applied) potential field Fo (see Equation 8.7) is
McNeal assumed that the potential on the extracellular side of the nodal membrane was fixed by the stimulating field. Since the latter is a point source (i.e., a monopole), the stimulating (applied) potential field Fo (see Equation 8.7) is

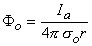
(21.2)
where Fo = stimulating (applied, extracellular) potential field [mV] Ia = applied current [µA] so = extracellular conductivity of the medium [kW·cm] r = distance from any node to the point source [cm]  On the basis of the network described in Figure 21.2 and the applied field of Equation 21.2 one can determine the response to step currents of varying strengths (up to that required for excitation at node 0). The equations that must be solved are based on Kirchhoff's laws. Letting subscript i denote intracellular, o extracellular, and n the index denoting a specific node (where the central node is designated 0), we have for the transmembrane current Im per nodal area at the nth node
On the basis of the network described in Figure 21.2 and the applied field of Equation 21.2 one can determine the response to step currents of varying strengths (up to that required for excitation at node 0). The equations that must be solved are based on Kirchhoff's laws. Letting subscript i denote intracellular, o extracellular, and n the index denoting a specific node (where the central node is designated 0), we have for the transmembrane current Im per nodal area at the nth node

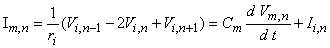
(21.3)
where Im, n = transmembrane current per nodal area at the nth node Ii, n = transmembrane ionic current per nodal area at the nth node Vm, n = transmembrane voltage at the nth node Cm = membrane capacitance per nodal area at the nth node ri = axial intracellular resistance per internodal length

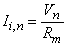
(21.4)
where Rm, n = transmembrane resistance per nodal area (constant)

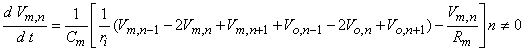
(21.5)

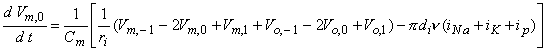
(21.6)  The solution of Equation 21.5 (for subthreshold conditions) or Equation 21.5 and 21.6 (for near-threshold conditions) at n = 0 requires temporal discretization and the solution of the resulting system of equations by iteration or by matrix techniques. The steady-state response to the stimulus diminishes rapidly with increasing values of n so that only a finite number of nodes (i.e., equations) need to be considered. One wishes to use the smallest number; McNeal (1976) explored the use of a total of 11, 21, and 31 nodes and found that the response to a 1 ms pulse was within 0.2 % accuracy with only 11 nodes.
The solution of Equation 21.5 (for subthreshold conditions) or Equation 21.5 and 21.6 (for near-threshold conditions) at n = 0 requires temporal discretization and the solution of the resulting system of equations by iteration or by matrix techniques. The steady-state response to the stimulus diminishes rapidly with increasing values of n so that only a finite number of nodes (i.e., equations) need to be considered. One wishes to use the smallest number; McNeal (1976) explored the use of a total of 11, 21, and 31 nodes and found that the response to a 1 ms pulse was within 0.2 % accuracy with only 11 nodes.
 The response to a subthreshold (at all nodes) current step evaluated at the central node and its four neighbors is described in Figure 21.3. These were calculated from a total of 31 nodes using the same parameters as were chosen by McNeal (see Table 21.1); the results appear to be identical to those obtained by McNeal with 11 nodes. Since the stimulus monopole was assumed to be cathodal, current must leave from the closest node(s) while, to conserve current, current must enter lateral nodes. This accounts for hyperpolarization of nodes ±2, ±3, ±4 . . . and depolarization of the central node. The behavior of node ±1 changes as the membrane capacitances charge up. Initially it is hyperpolarized, but its steady-state potential (response to a pulse of very long duration) is a depolarization. If the stimulus were anodal, then the signs of all responses in Figure 21.3 would be reversed; the initial largest depolarization occurs at node ±1, but after around 15 ms the largest depolarization is at ±2. Thus excitation resulting from a stimulus duration of t
The response to a subthreshold (at all nodes) current step evaluated at the central node and its four neighbors is described in Figure 21.3. These were calculated from a total of 31 nodes using the same parameters as were chosen by McNeal (see Table 21.1); the results appear to be identical to those obtained by McNeal with 11 nodes. Since the stimulus monopole was assumed to be cathodal, current must leave from the closest node(s) while, to conserve current, current must enter lateral nodes. This accounts for hyperpolarization of nodes ±2, ±3, ±4 . . . and depolarization of the central node. The behavior of node ±1 changes as the membrane capacitances charge up. Initially it is hyperpolarized, but its steady-state potential (response to a pulse of very long duration) is a depolarization. If the stimulus were anodal, then the signs of all responses in Figure 21.3 would be reversed; the initial largest depolarization occurs at node ±1, but after around 15 ms the largest depolarization is at ±2. Thus excitation resulting from a stimulus duration of t 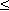 15 ms and that for t >15 ms occur at different nodes!
15 ms and that for t >15 ms occur at different nodes!
| Symbol | Parameter | Value |
| ri | axoplasm resistivity | 0.11 kW·cm |
| ro | extracellular resistivity | 0.3 kW·cm |
| Cm | nodal membrane capacitance/unit area | 2.0 µF/cm2 |
| Gm | nodal membrane conductance/unit area | 0.4 mS/cm² |
| n | nodal gap width | 0.5 µm |
| l / do | ratio of internode spacing to fiber diameter | 100 |
| di / do | ratio of axon diameter (internal myelin) to fiber diameter | 0.7 |
| Rmn | nodal membrane resistance = 1/(Gmpdin) | 29.9 MW |
| Cmn | nodal membrane capacitance = Cmpdin | 2.2 pF |
| ril | internodal resistance = 4ri l /(pdi2) | 14.3 MW |
Figure 21.3 Response at central node (n = 0) and adjoining four nodes to a point current source located 1 mm from the fiber and excited with a current step of 0.1 mA. The geometry is described in Figure 21.1. The fiber diameter is 20 µm, and the internodal spacing is 2 mm. Other parameters are given in Table 21.1.
 Returning to the case of cathodal stimulation, it is clear that for a transthreshold stimulus, activation occurs at node 0. A determination of the quantitative values of current strength and duration to achieve activation requires (at least) the use of Equation 21.6 to describe the central node. McNeal was able to calculate that for a 100 ms pulse the threshold current is 0.23 mA. By determinination of the corresponding threshold current for a series of different pulse durations, an experimental strength-duration curve (reproduced in Figure 21.4) was constructed. This curve describes conditions under which excitation is just achieved for the specific case of a 20 µm fiber with a point source at a distance of 1 mm. Under the idealized conditions described in Chapter 3, we expect this curve to have a slope of -1 for small pulse duration, but this is not the case in an experimental curve. The reason for this discrepancy is that the experiment is affected by accommodation, distributed fiber structure, and source geometry.
Returning to the case of cathodal stimulation, it is clear that for a transthreshold stimulus, activation occurs at node 0. A determination of the quantitative values of current strength and duration to achieve activation requires (at least) the use of Equation 21.6 to describe the central node. McNeal was able to calculate that for a 100 ms pulse the threshold current is 0.23 mA. By determinination of the corresponding threshold current for a series of different pulse durations, an experimental strength-duration curve (reproduced in Figure 21.4) was constructed. This curve describes conditions under which excitation is just achieved for the specific case of a 20 µm fiber with a point source at a distance of 1 mm. Under the idealized conditions described in Chapter 3, we expect this curve to have a slope of -1 for small pulse duration, but this is not the case in an experimental curve. The reason for this discrepancy is that the experiment is affected by accommodation, distributed fiber structure, and source geometry.
 The dependence of excitability on the fiber diameter of a nerve is important since it describes how a nerve bundle (consisting of fibers of different diameter) will respond to a stimulus (monopole in this case). An examination of Equations 21.5 and 21.6 shows that changes in fiber diameter do affect the solution only through its link with the internodal spacing, l. Figure 21.5 gives the threshold current for a monopole at a distance of 1 mm from a fiber whose diameter do satisfies (2 µm
The dependence of excitability on the fiber diameter of a nerve is important since it describes how a nerve bundle (consisting of fibers of different diameter) will respond to a stimulus (monopole in this case). An examination of Equations 21.5 and 21.6 shows that changes in fiber diameter do affect the solution only through its link with the internodal spacing, l. Figure 21.5 gives the threshold current for a monopole at a distance of 1 mm from a fiber whose diameter do satisfies (2 µm  do
do  25 µm) where the pulse duration is 100 µs. A 10-fold decrease in diameter (from 20 to 2 µm) affects ri and Rm proportionately (each increases by 10). As a rough approximation the induced transmembrane voltage at node 0 is the same fraction of the applied potential difference between nodes zero and 1. This potential decreases quite considerably for the 2 µm diameter nerve versus the 20 µm diameter one since l is 10 times greater in the latter case. Accordingly the excitability is expected to decrease for the nerve of lower diameter. Figure 21.5 confirms this effect through the simulation. Note that at the larger diameters the slope is around -½, meaning that the threshold is approximately inversely proportional to the square root of the fiber diameter.
25 µm) where the pulse duration is 100 µs. A 10-fold decrease in diameter (from 20 to 2 µm) affects ri and Rm proportionately (each increases by 10). As a rough approximation the induced transmembrane voltage at node 0 is the same fraction of the applied potential difference between nodes zero and 1. This potential decreases quite considerably for the 2 µm diameter nerve versus the 20 µm diameter one since l is 10 times greater in the latter case. Accordingly the excitability is expected to decrease for the nerve of lower diameter. Figure 21.5 confirms this effect through the simulation. Note that at the larger diameters the slope is around -½, meaning that the threshold is approximately inversely proportional to the square root of the fiber diameter.
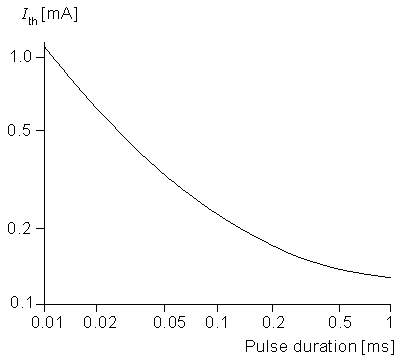
Figure 21.4 Log-log plot of a strength duration that just produces activation of 20 µm diameter myelinated fiber from a point source of current 1 mm distant. The geometry is described in Figure 21.1, and the fiber electrical properties are tabulated in Table 21.1. (From McNeal, 1976.)
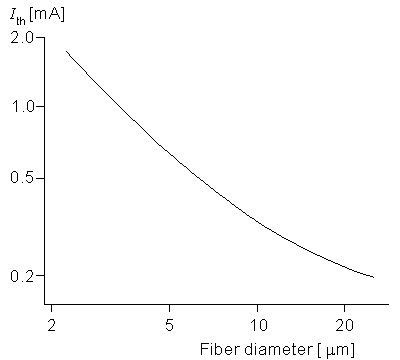
- Figure 21.5 Log-log plot of the relationship between threshold current and myelinated fiber diameter for a point current source 1 mm from the fiber. The geometry is described in Figure 21.1, and the fiber electrical properties are given in Table 21.1. (From McNeal, 1976.)
21.3 STIMULATION OF AN UNMYELINATED AXON
The response of a single unmyelinated fiber to a stimulating field can be found through the same type of simulation described for the myelinated fiber. In fact, to obtain numerical solutions it is necessary to discretize the axial coordinate (x) into elements Dx and a network somewhat similar to that considered in Figure 21.2 results. One obtains an expression for the transmembrane current at the nth element, from the cable equations, as
 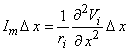 | (21.7) |
| ri | = the intracellular axial resistance per unit length. |
 Approximating the second derivative in Equation 21.7 by second differences gives us
Approximating the second derivative in Equation 21.7 by second differences gives us
 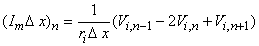 | (21.8) |
| Vi,n | = intracellular potential at the nth element, etc. |
 The desired equation is found by equating the transmembrane current evaluated from Equation 21.8 (which is determined by the fiber structure) with that demanded by the intrinsic nonlinear membrane properties:
The desired equation is found by equating the transmembrane current evaluated from Equation 21.8 (which is determined by the fiber structure) with that demanded by the intrinsic nonlinear membrane properties:
 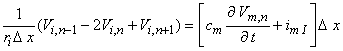 | (21.9) |
| cm | = membrane capacitance per unit length | |
| imI | = ionic component of the membrane current per unit length |
The ionic currents are those of sodium, potassium, and chloride ions, as found from Hodgkin and Huxley (1952) and so on.
(Note that had we assumed steady-state conditions, the capacitive term could be set equal to zero, whereas if linear conditions could be assumed, then imI = Vm,n/Rm.) If, now, we replace Vi,n by Vm,n + Vo,n and reorganize, we have
 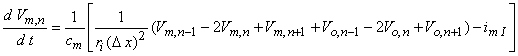 | (21.10) |
which is essentially the same as Equation 21.6 except that the spacing between elements in Equation 21.10, namely Dx, may be much smaller than the spacing in Equation 21.6, namely l. Of course, the internodal spacing is set by the myelinated histology while Dx is at our disposal.
and note that for anodal excitation, depolarization results only for | x |
 The forcing function in Equation 21.10 is essentially
The forcing function in Equation 21.10 is essentially  2Vo/
2Vo/ x2. Depending on the spatial behavior of Vo and the length l, the forcing function in Equation 21.6 is also given approximately by
x2. Depending on the spatial behavior of Vo and the length l, the forcing function in Equation 21.6 is also given approximately by  2Vo/
2Vo/ x2. We have noted that Vo is normally the field of the stimulating electrodes in the absence of the stimulated fiber. That is, for a single isolated fiber its (secondary) effect on the axial field in which it is placed is, ordinarily, negligible, as discussed earlier. So
x2. We have noted that Vo is normally the field of the stimulating electrodes in the absence of the stimulated fiber. That is, for a single isolated fiber its (secondary) effect on the axial field in which it is placed is, ordinarily, negligible, as discussed earlier. So  2Vo/
2Vo/ x2 can be evaluated from the field of the stimulating electrodes alone. Clearly, the response to a stimulating field is contained in this second-derivative behavior, designated the "activating function" by Rattay
(1986). In fact, for the linear behavior that necessarily precedes excitation, Equation 21.10 may be replaced by the following equation (an approximation that improves as Dx
x2 can be evaluated from the field of the stimulating electrodes alone. Clearly, the response to a stimulating field is contained in this second-derivative behavior, designated the "activating function" by Rattay
(1986). In fact, for the linear behavior that necessarily precedes excitation, Equation 21.10 may be replaced by the following equation (an approximation that improves as Dx  0, hence less satisfactory for myelinated fibers where Dx = l )
0, hence less satisfactory for myelinated fibers where Dx = l )

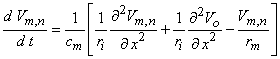
(21.11)
rm = membrane resistance per unit length (resistance times length) ri = intracellular axial resistance per unit length  We consider the response, Vm,n, to a stimulating field, Vo, which is turned on at t = 0 (i.e., a step function). Activation is possible if
We consider the response, Vm,n, to a stimulating field, Vo, which is turned on at t = 0 (i.e., a step function). Activation is possible if  Vm,n/
Vm,n/ t > 0, and this condition in turn seems to depend on
t > 0, and this condition in turn seems to depend on  2Vo/
2Vo/ x2 > 0. Rattay assumed this relationship to be valid and designated
x2 > 0. Rattay assumed this relationship to be valid and designated  2Vo/
2Vo/ x2 as an "activating function." An application, given by Rattay, is described below. However, the reader should note that Vm,n is not directly dependent on
x2 as an "activating function." An application, given by Rattay, is described below. However, the reader should note that Vm,n is not directly dependent on  2Vo/
2Vo/ x2 but, rather, arises from it only through the solution of Equation 21.11. But this solution also depends on the homogeneous solution plus the boundary conditions. That the outcome of the same forcing function can vary in this way suggests that the interpretation of
x2 but, rather, arises from it only through the solution of Equation 21.11. But this solution also depends on the homogeneous solution plus the boundary conditions. That the outcome of the same forcing function can vary in this way suggests that the interpretation of  2Vo/
2Vo/ x2 as an activating function is not assured.
x2 as an activating function is not assured.
 Figure 21.6 shows the applied field Vo(x) along an unmyelinated fiber for a point source that is 1 mm distant, and the corresponding activating function for both an anodal and a cathodal condition. For a negative (cathodal) current of -290 µA, threshold conditions are just reached at the fiber element lying at the foot of the perpendicular from the monopole (which is at the location of the positive peak of the plotted
Figure 21.6 shows the applied field Vo(x) along an unmyelinated fiber for a point source that is 1 mm distant, and the corresponding activating function for both an anodal and a cathodal condition. For a negative (cathodal) current of -290 µA, threshold conditions are just reached at the fiber element lying at the foot of the perpendicular from the monopole (which is at the location of the positive peak of the plotted  2Vo/
2Vo/ x2 curve). For a positive (anodal) current source, 1450 µA is required just to reach excitation; this is seen in the curve of the corresponding activating function (d2Vo/dx2) that results. The fivefold increase in current compensates for the lateral peaks in the activating function, being only one-fifth of the central peak. The location of the excitation region can be found from Equation 21.2 written as
x2 curve). For a positive (anodal) current source, 1450 µA is required just to reach excitation; this is seen in the curve of the corresponding activating function (d2Vo/dx2) that results. The fivefold increase in current compensates for the lateral peaks in the activating function, being only one-fifth of the central peak. The location of the excitation region can be found from Equation 21.2 written as

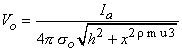
(21.12)
h = distance from the point source to the fiber x = axial distance along fiber so = conductance of the extracellular medium  We examine the lateral behavior of
We examine the lateral behavior of

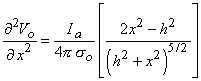
(21.13)  h /
h /  2 (hyperpolarization is produced for | x |
2 (hyperpolarization is produced for | x | 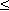 h /
h / 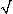 2). Conversely, activation from cathodal stimulation is confined to the region | x |
2). Conversely, activation from cathodal stimulation is confined to the region | x | 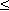 h /
h / 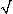 2, while hyperpolarization is produced laterally.
2, while hyperpolarization is produced laterally.
 For cathodal stimulation and for increasing stimulus intensity, a threshold level is reached that results in activation. A continued increase in stimulus intensity is followed by little change in behavior until a level some eight times threshold is reached. At this point the hyperpolarization lateral to the active region can block the emerging propagating impulse. Rattay (1987) investigated this behavior quantitatively by solving Equation 21.10 with the ionic currents evaluated from the Hodgkin-Huxley equations and with the point source field of Equation 21.12. The results are plotted in Figure 21.7 for an unmyelinated fiber of 9.6 µm diameter (inner scales) and 38.4 µm diameter (outer scales).
For cathodal stimulation and for increasing stimulus intensity, a threshold level is reached that results in activation. A continued increase in stimulus intensity is followed by little change in behavior until a level some eight times threshold is reached. At this point the hyperpolarization lateral to the active region can block the emerging propagating impulse. Rattay (1987) investigated this behavior quantitatively by solving Equation 21.10 with the ionic currents evaluated from the Hodgkin-Huxley equations and with the point source field of Equation 21.12. The results are plotted in Figure 21.7 for an unmyelinated fiber of 9.6 µm diameter (inner scales) and 38.4 µm diameter (outer scales).
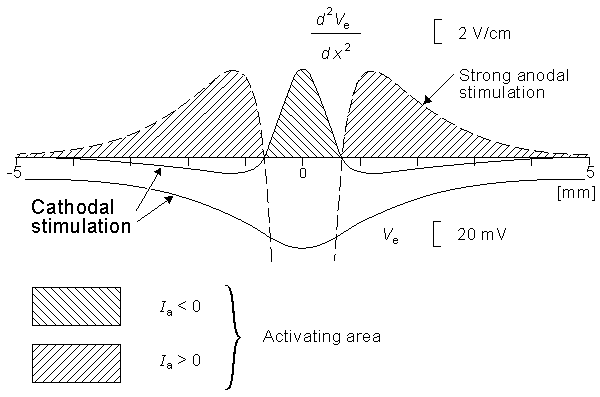
Figure 21.6 The cathodal applied field Vo(x) along a fiber oriented along x due to a point source, and  2Vo(x)/
2Vo(x)/ x2 for both cathodal and anodal stimuli. The cathodal threshold current of -290 µA initiates activation at x = 0 which corresponds to the peak of the "activating function"
x2 for both cathodal and anodal stimuli. The cathodal threshold current of -290 µA initiates activation at x = 0 which corresponds to the peak of the "activating function"  2Vo(x)/
2Vo(x)/ x2. For anodal conditions the stimulus for threshold activation is 1450 µA and the corresponding activating function is shown. The fivefold increase in current is required to bring the corresponding (anodal) positive peak of
x2. For anodal conditions the stimulus for threshold activation is 1450 µA and the corresponding activating function is shown. The fivefold increase in current is required to bring the corresponding (anodal) positive peak of  2Vo/
2Vo/ x2 to the same level it has under threshold cathodal conditions. Note that excitation takes place at x lateral to the point 0. (From Rattay, 1986.)
x2 to the same level it has under threshold cathodal conditions. Note that excitation takes place at x lateral to the point 0. (From Rattay, 1986.)
 Figure 21.7 may be explained as follows. For a cathodal stimulus of -4 mA and the smaller-diameter fiber (use inner coordinate scale), excitation occurs (cross-hatched region) if the source-field distance rages from 0.73 to 1.55 mm (following line (A)) whereas for the larger fiber, excitation requires the source-field distance to lie between 0.94 and 2.44 mm (following line (B)). The spherical insets describe the relative minimum and maximum radii for excitation of the smaller fiber (A) and larger fiber. Consistent with the results obtained with myelinated fibers, we note the greater excitability of the larger fiber, where excitation can be initiated at a maximum distance of 2.44 mm compared with 1.55 mm for a fiber with one-fourth the diameter. For a bundle of fibers of different diameters and radial position, with no fiber interaction (i.e., each fiber behaves as if isolated), Figure 21.7 could describe the selective effect of any given level of stimulation of a fiber at a specified position.
Figure 21.7 may be explained as follows. For a cathodal stimulus of -4 mA and the smaller-diameter fiber (use inner coordinate scale), excitation occurs (cross-hatched region) if the source-field distance rages from 0.73 to 1.55 mm (following line (A)) whereas for the larger fiber, excitation requires the source-field distance to lie between 0.94 and 2.44 mm (following line (B)). The spherical insets describe the relative minimum and maximum radii for excitation of the smaller fiber (A) and larger fiber. Consistent with the results obtained with myelinated fibers, we note the greater excitability of the larger fiber, where excitation can be initiated at a maximum distance of 2.44 mm compared with 1.55 mm for a fiber with one-fourth the diameter. For a bundle of fibers of different diameters and radial position, with no fiber interaction (i.e., each fiber behaves as if isolated), Figure 21.7 could describe the selective effect of any given level of stimulation of a fiber at a specified position.
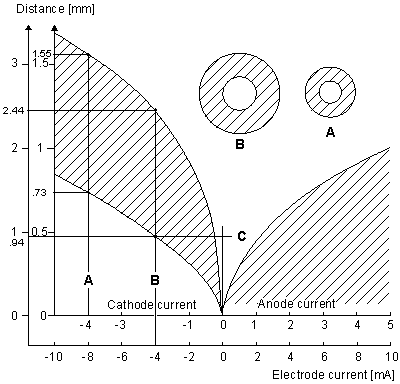
Figure 21.7 Current-distance relationship for unmyelinated fibers. Excitation occurs for points lying in the shaded region. For cathodal stimulation, a minimum distance arises at the point where anodal block prevents the escape of the action impulse. For anodal stimulation, block does not occur; thus there is no lower limit on the source-fiber distance. The inner scales are for a fiber diameter of 9.6 µm, and the outer for a diameter of 38.4 µm. (An examination of Equations 21.10 and 21.13 shows that scaling the excitation with respect to both current strength, source-fiber distance, and fiber diameter leaves the solution unchanged.) (From Rattay, 1987.)
21.4 MUSCLE RECRUITMENT
If a muscle fiber is electrically stimulated, it responds with a twitch, as shown in Figure 21.8. If a train of stimuli is supplied whose time interval is shorter than the twitch duration, then temporal summation will occur and a larger tensile force will be developed. For a high enough frequency a smooth (rather than bumpy) tension response is observed (this is the fusion frequency), leading to a maximum (tetanus) contraction. The magnitude and duration of the twitch response differ depending on the muscle fiber type. One can separate skeletal muscle into three general groups according to their physiological and metabolic properties (Mortimer, 1981):
The magnitude and duration of the twitch response differ depending on the muscle fiber type. One can separate skeletal muscle into three general groups according to their physiological and metabolic properties (Mortimer, 1981):
Fast twitch, glycolytic (FG): These fibers depend mainly on glycolytic metabolism with little oxidative. When stimulated, the twitch contraction is of short duration and the response to repeated stimulation shows a rapid fatigue and slow recovery. In a mixed muscle this fiber tends to be found near the periphery. The fiber diameter is relatively large, as is the relative strength of its peak force (for cat gastrocnemius a peak force of 1.5- 2.0 kg/cm2 of muscle cross-sectional area is reached).
Fast twitch, oxidative (FO): Distinct from the FG group are the fast twitch oxidative, which utilize both oxidative as well as glycolytic metabolism. The response to repeated stimulation is slower to fatigue and quicker to recover than for the FG fiber type. The diameter of the FO fiber is smaller than the FG while its peak force is on the order of 2.6-2.9 kg/cm2 of muscle cross-sectional area for cat gastrocnemius.
Slow twitch, oxidative (SO): These fibers have the smallest cross-sectional area of the three groups. They have a low capacity for glycolytic metabolism. Their twitch response is longest in duration and lowest in magnitude (the fusion frequency is the lowest) of the three groups. Repeated stimulation causes less fatigue, and recovery is rapid. These fiber tend to lie in the central region of a muscle bundle. In the cat gastrocnemius, they generate a peak force of around 0.6 kg/cm2.
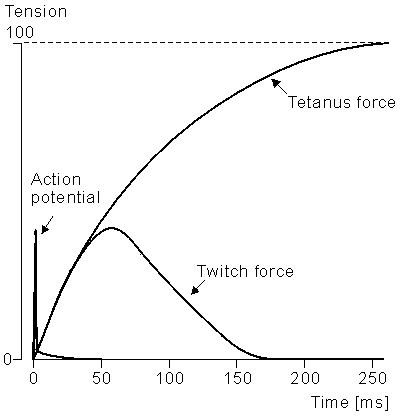
Figure 21.8 The twitch response (tension vs. time) for a single muscle fiber. The stimulus is described by the initial impulse.
 Each fiber in a bundle is innervated by a single motor neuron, but each motor neuron activates several fibers. The group of fibers activated by a single motor neuron is called a motor unit. All fibers in a motor unit are of a similar type. Not surprisingly large-diameter muscle fibers are innervated by large- diameter neurons. Consequently, motor units producing the largest forces are those innervated by axons of large diameter; conversely, small forces are produced by small-diameter axons. The natural order of recruitment is the development of small forces from SO fibers followed, ultimately, by the largest forces due to recruitment of the FG motor units. The FO fibers contribute in the midrange. Thus the modest forces needed to maintain posture for a long period are derived from the SO type fiber, whereas the baseball batter's swing describes the momentary recruitment of FG fibers (for a large force of short duration whose fatigue and slow recovery is of less consequence). Other more conventional physiological tasks have this same character, as seen in baseball.
Each fiber in a bundle is innervated by a single motor neuron, but each motor neuron activates several fibers. The group of fibers activated by a single motor neuron is called a motor unit. All fibers in a motor unit are of a similar type. Not surprisingly large-diameter muscle fibers are innervated by large- diameter neurons. Consequently, motor units producing the largest forces are those innervated by axons of large diameter; conversely, small forces are produced by small-diameter axons. The natural order of recruitment is the development of small forces from SO fibers followed, ultimately, by the largest forces due to recruitment of the FG motor units. The FO fibers contribute in the midrange. Thus the modest forces needed to maintain posture for a long period are derived from the SO type fiber, whereas the baseball batter's swing describes the momentary recruitment of FG fibers (for a large force of short duration whose fatigue and slow recovery is of less consequence). Other more conventional physiological tasks have this same character, as seen in baseball.
 The strength-duration curves for the stimulation of a motor nerve and the direct stimulation of muscle are shown in Figure 21.9. We note the very great difference in excitability so that, for the most part, all functional electric stimulation (FES) systems concentrate on the stimulation of the motor neuron which, in turn, activates the associated muscle. One may stimulate the nerve centrally or peripherally (in the vicinity of the neuromuscular junction). The latter has the advantage, usually, of greater selectivity.
The strength-duration curves for the stimulation of a motor nerve and the direct stimulation of muscle are shown in Figure 21.9. We note the very great difference in excitability so that, for the most part, all functional electric stimulation (FES) systems concentrate on the stimulation of the motor neuron which, in turn, activates the associated muscle. One may stimulate the nerve centrally or peripherally (in the vicinity of the neuromuscular junction). The latter has the advantage, usually, of greater selectivity.
 Figures 21.5 and 21.7 show that with point-source stimulation the excitability increases with increasing fiber diameter. This relationship is true in general regardless of the type of electrode system or placement relative to the target nerve. But this means that the large-diameter neurons, - hence large-diameter muscle fibers (i.e., FG) - are recruited first. This is inverse to the natural order and results in the excitation of a fiber type with rapid fatigue for ordinary tasks. This result is a serious limitation to the applicability of FES.
Figures 21.5 and 21.7 show that with point-source stimulation the excitability increases with increasing fiber diameter. This relationship is true in general regardless of the type of electrode system or placement relative to the target nerve. But this means that the large-diameter neurons, - hence large-diameter muscle fibers (i.e., FG) - are recruited first. This is inverse to the natural order and results in the excitation of a fiber type with rapid fatigue for ordinary tasks. This result is a serious limitation to the applicability of FES.
 Several approaches have been taken to deal with the problem noted above. The first is to devise a technique that will result in the electric stimulation of the smaller-diameter nerve fiber before the larger-diameter one. For example, one can first stimulate all fibers with a supramaximal pulse and then at a point closer to the muscle place a hyperpolarizing block. One adjusts the strength of the block to be inversely proportional to the desired control signal. Since larger-diameter fibers are most easily blocked, a low control signal - hence a large block - will block all but the smallest fibers, whereas increasing force reguirements will result in reduced block (permitting the FO and finally the FG to escape block). Consequently, the behavior follows more closely the natural recruitment order (Zhou, Baratta, and Solomonow, 1987), though there are still a number of practical difficulties with the application of this method. An alternate application of the technique, which depends on the use of a quasi-trapezoidal stimulus current, appears to achieve a natural order of recruitment (Fang and Mortimer, 1987).
Several approaches have been taken to deal with the problem noted above. The first is to devise a technique that will result in the electric stimulation of the smaller-diameter nerve fiber before the larger-diameter one. For example, one can first stimulate all fibers with a supramaximal pulse and then at a point closer to the muscle place a hyperpolarizing block. One adjusts the strength of the block to be inversely proportional to the desired control signal. Since larger-diameter fibers are most easily blocked, a low control signal - hence a large block - will block all but the smallest fibers, whereas increasing force reguirements will result in reduced block (permitting the FO and finally the FG to escape block). Consequently, the behavior follows more closely the natural recruitment order (Zhou, Baratta, and Solomonow, 1987), though there are still a number of practical difficulties with the application of this method. An alternate application of the technique, which depends on the use of a quasi-trapezoidal stimulus current, appears to achieve a natural order of recruitment (Fang and Mortimer, 1987).
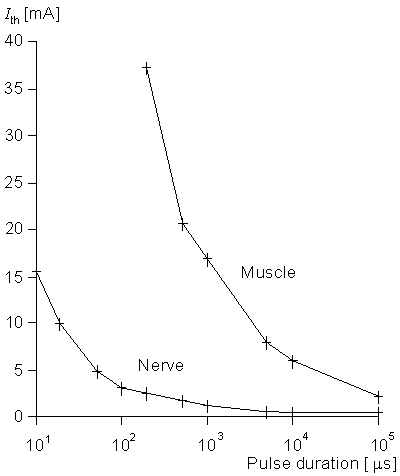
Figure 21.9 Experimentally determined strength-duration relationship for motor nerve stimulation and for direct stimulation of the muscle. In each case the muscle response was held at the same constant value (a relatively low level of force). (From Mortimer, 1981.)
 A second approach is to implant several electrodes each in a different part of the muscle and to excite them sequentially. In this way, the actual stimulus frequency of each subunit is reduced by a factor equal to the number of electrodes. Since spatial summation results, the behavior of the whole muscle is characterized by the higher frequency which is chosen to exceed the fusion frequency. The lower actual frequency results in reduced fatigue of the muscle. The method is referred to as "roundabout stimulation" (Holle et al., 1984).
A second approach is to implant several electrodes each in a different part of the muscle and to excite them sequentially. In this way, the actual stimulus frequency of each subunit is reduced by a factor equal to the number of electrodes. Since spatial summation results, the behavior of the whole muscle is characterized by the higher frequency which is chosen to exceed the fusion frequency. The lower actual frequency results in reduced fatigue of the muscle. The method is referred to as "roundabout stimulation" (Holle et al., 1984).
 A third approach has been to convert FG muscle into SO muscle by a period of electrical stimulation. The results of a daily regimen of "exercise" over a 4-week period include a decrease in fusion frequency from 40 to 10 Hz and an improved ability to maintain force. In fact, analysis of such stimulated muscle shows histochemical changes consistent with a transition from fast twitch to slow twitch. In addition, one also sees a marked increase in the number of capillaries per fiber consistent with an increased capacity for oxidative metabolism (Mortimer, 1981).
A third approach has been to convert FG muscle into SO muscle by a period of electrical stimulation. The results of a daily regimen of "exercise" over a 4-week period include a decrease in fusion frequency from 40 to 10 Hz and an improved ability to maintain force. In fact, analysis of such stimulated muscle shows histochemical changes consistent with a transition from fast twitch to slow twitch. In addition, one also sees a marked increase in the number of capillaries per fiber consistent with an increased capacity for oxidative metabolism (Mortimer, 1981).
21.5 ELECTRODE-TISSUE INTERFACE
A discussion of electric stimulation of tissue would be clearly incomplete without a consideration of electrodes and their behavior. In this context since a replacement of the charge carrier from conduction electron in the metal electrode to ion in the tissue must occur at the electrode-tissue interface, a consideration of the electrochemistry and its relationship to electrode material and shape is important. In addition, we need to touch upon the mechanical properties of electrodes, as they too are influenced by material and shape.
 There is extensive literature on the electrochemistry at the metal-electrolyte interface (Conway, 1965). For our purposes, here, we call attention to the equivalent electric circuit depicted in Figure 21.10 which summarizes the electrode tissue behavior (Dymond, 1976). The capacitance reflects the double layer of charge that arises at the metal-electrolyte interface; the single layer in the metal arises because of its connection to the battery, whereas that in the electrolyte is due to the attraction of ions in the electric field. These layers are separated by the molecular dimensions of the water molecule so the effective capacitance (being inversely proportional to charge separation) is quite high.
There is extensive literature on the electrochemistry at the metal-electrolyte interface (Conway, 1965). For our purposes, here, we call attention to the equivalent electric circuit depicted in Figure 21.10 which summarizes the electrode tissue behavior (Dymond, 1976). The capacitance reflects the double layer of charge that arises at the metal-electrolyte interface; the single layer in the metal arises because of its connection to the battery, whereas that in the electrolyte is due to the attraction of ions in the electric field. These layers are separated by the molecular dimensions of the water molecule so the effective capacitance (being inversely proportional to charge separation) is quite high.
 At sufficiently low levels the current will be primarily capacitive with little or no flow through the pathway represented by the Faradic impedance Z in Figure 21.10. But for high currents that exceed the capabilities of the capacitance channel, irreversible chemical reactions will take place, and these are reflected in Figure 21.10 by a much reduced impedance Z. The consequences of these chemical reactions are undesirable since they are detrimental to the tissue or electrode or both.
At sufficiently low levels the current will be primarily capacitive with little or no flow through the pathway represented by the Faradic impedance Z in Figure 21.10. But for high currents that exceed the capabilities of the capacitance channel, irreversible chemical reactions will take place, and these are reflected in Figure 21.10 by a much reduced impedance Z. The consequences of these chemical reactions are undesirable since they are detrimental to the tissue or electrode or both.
 In general, the goal is to operate stimulating electrodes to utilize exclusively their capacitance and thereby to keep within their operating (linear) range. Under these conditions the electrode current is, essentially capacitive and reversible; in this way one can avoid detrimental chemical reactions. For example, if a stainless steel electrode is excessively anodic one gets
In general, the goal is to operate stimulating electrodes to utilize exclusively their capacitance and thereby to keep within their operating (linear) range. Under these conditions the electrode current is, essentially capacitive and reversible; in this way one can avoid detrimental chemical reactions. For example, if a stainless steel electrode is excessively anodic one gets
 Fe Fe  Fe2+ + 2e¯ Fe2+ + 2e¯ | (2.14) |
and the dissolution of the electrode results. For an excessively cathodic condition the result is
 2H2O + 2e¯ 2H2O + 2e¯  H2 + 2OH¯ H2 + 2OH¯ | (2.15) |
and increasingly negative electrode may result in
 O2 + H2O + 2e¯ O2 + H2O + 2e¯  OH¯ + O2H¯ OH¯ + O2H¯ | (2.16) |
In either case a consequent rise in pH results which can produce tissue damage.
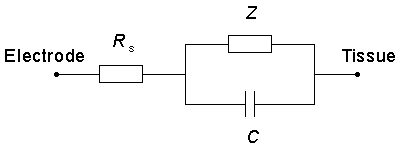
Figure 21.10 The electrode-tissue interface includes a series ohmic resistance Rs, a series capacitance Cs, and a Faradaic impedance Z. The capacitance represents a double layer that arises at the metal-electrolyte interface, whereas the Faradaic impedance includes several physical and chemical processes that may occur.
Chu SY, Ritchie JM (1984): On the physiological role of internodal potassium channels and the security of conduction in myelinated nerve fibers. Proc. Roy. Soc. (London) B220: 415-22.
Conway BE (1965): Theory and Principles of Electrode Processes, 303 pp. Ronald, New York.
Dymond AM (1976): Characteristics of the metal-tissue interface of stimulation electrodes. IEEE Trans. Biomed. Eng. BME-23:(4) 274-80.
Fang ZB, Mortimer JT (1987): A method for attaining natural recruitment order in artificially activated muscles. In Proc. Ninth Annual Conf. IEEE Eng. In Med. And Biol. Society, Vol. 2, ., pp. 657-8, IEEE Press, New York.
Frankenhauser B, Huxley AF (1964): The action potential in the myelinated nerve fibre of Xenopus Laevis as computed on the basis of voltage clamp data. J. Physiol. (Lond.) 171: 302-15.
Hodgkin AL, Huxley AF (1952): A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 117: 500-44.
Holle J, Frey M, Gruber H, Kern H, Stöhr H, Thoma H (1984): Functional electrostimulation of paraplegics. Orthop. 7: 1145-55.
McNeal DR (1976): Analysis of a model for excitation of myelinated nerve. IEEE Trans. Biomed. Eng. BME-23:(4) 329-37.
Mortimer JT (1981): Motor prostheses. In Handbook of Physiology, Section 1: The Nervous System. Motor Control Part I, Vol. II, ., pp. 155-87, American Physiological Society, Bethesda, Md.
Plonsey R (1974): The active fiber in a volume conductor. IEEE Trans. Biomed. Eng. BME-21:(5) 371-81.
Rattay F (1986): Analysis of models for external stimulation of axons. IEEE Trans. Biomed. Eng. BME-33:(10) 974-7.
Rattay F (1987): Ways to approximate current-distance relations for electrically stimulated fibers. J. Theor. Biol. 125: 339-49.
Seligman LJ (1982): Physiological stimulators: From electric fish to programmable implants. IEEE Trans. Biomed. Eng. BME-29:(4) 270-84.
Talonen P, Malmivuo JA, Baer G, Markkula H, Häkkinen V (1983): Transcutaneous, dual channel phrenic nerve stimulator for diaphragm pacing. Med. & Biol. Eng. & Comput. 21:(1) 21-30.
Zhou B-H, Baratta R, Solomonow M (1987): Manipulation of muscle force with various firing rate and recruitment control strategies. IEEE Trans. Biomed. Eng. BME-34:(2) 128-39.
Eccles JC, Dimitrijevic MR (eds.) (1985): Upper Motor Neuron Functions and Dysfunctions, 345 pp. S. Karger, Basel.
Hambrecht FT, Reswick JB (eds.) (1977): Functional Electrical Stimulation. Application in Neural Prosthesis, Vol. 3, 543 pp. Marcel Dekker, N.Y.
Lazorthes Y, Upton ARM (eds.) (1985): Neurostimulation: An Overview, 320 pp. Futura, Mount Kisco, N.Y.
Mannheimer JS, Lampe GN (1987): Clinical Transcutaneous Electrical Nerve Stimulation, 636 pp. F.A. Davis, Philadelphia.
Myklebust JB, Cusick JF, Sances AJ, Larson SJ (eds.) (1985): Neural Stimulation, Vol. I and II, 158+160 pp. CRC Press, Boca Raton, Fla.
Reilly JP (1992): Electrical Stimulation & Electropathology, 504 pp. Cambridge University Press, Cambridge.
Wolf SL (ed.) (1981): Electrotherapy, 204 pp. Churchill Livingstone, New York.
 Operating an electrode in its linear (capacitive) range is desirable since it is entirely reversible and results in neither tissue damage or electrode dissolution. To do so requires that the electrode be positioned as close as possible to the target nerve (so that the maximum required current will be minimal) and, if possible, to have a large area for a low current density. Finally the electrode material should be chosen to have maximum capacitance (other things being the same). A roughened surface appears to result in a decrease in microscopic current density without affecting the overall size of the electrode. The values of charge storage appears to increase from 0.5 to 2.0 µC/mm2, yet remain in the reversible region for platinum and stainless steel materials.
Operating an electrode in its linear (capacitive) range is desirable since it is entirely reversible and results in neither tissue damage or electrode dissolution. To do so requires that the electrode be positioned as close as possible to the target nerve (so that the maximum required current will be minimal) and, if possible, to have a large area for a low current density. Finally the electrode material should be chosen to have maximum capacitance (other things being the same). A roughened surface appears to result in a decrease in microscopic current density without affecting the overall size of the electrode. The values of charge storage appears to increase from 0.5 to 2.0 µC/mm2, yet remain in the reversible region for platinum and stainless steel materials.
 If the stimulating current is unipolar, then even though one pulse causes the storage of charge within the reversible range, subseguent pulses will eventually cause the operating point to move out of the reversible region. The reasons are that under the usual operating conditions accumulation of charge takes place but there is inadequate time for the charge to leak away. Thus practical stimulation conditions require the use of biphasic pulses. In fact, these must be carefully balanced to avoid an otherwise slow buildup of charge. A series capacitance will ensure the absence of DC components (Talonen et al., 1983).
If the stimulating current is unipolar, then even though one pulse causes the storage of charge within the reversible range, subseguent pulses will eventually cause the operating point to move out of the reversible region. The reasons are that under the usual operating conditions accumulation of charge takes place but there is inadequate time for the charge to leak away. Thus practical stimulation conditions require the use of biphasic pulses. In fact, these must be carefully balanced to avoid an otherwise slow buildup of charge. A series capacitance will ensure the absence of DC components (Talonen et al., 1983).
21.6 ELECTRODE MATERIALS AND SHAPES
For the most part FES utilizes electrodes that are implanted into the body since transcutaneous stimulation requires high current levels and may result in local tissue damage and unwanted nerve excitation. The electrode materials are therefore confined to those that are essentially inert such as platinum, platinum-iridium, and 316 stainless steel.
 Less trauma results from electrodes that are flexible; consequently, small-diameter wires are preferred. Rather than transverse bending of a straight wire, these may often be coiled into a helix since bending is converted into torsional rotation, hence reducing stress. In fact, the use of stranded wires represents a further useful step to reduce breakage (or to afford some redundancy if some wires should fail).
Less trauma results from electrodes that are flexible; consequently, small-diameter wires are preferred. Rather than transverse bending of a straight wire, these may often be coiled into a helix since bending is converted into torsional rotation, hence reducing stress. In fact, the use of stranded wires represents a further useful step to reduce breakage (or to afford some redundancy if some wires should fail).
 In the stimulation of the brain, of particular concern is preventing breakdown of the blood-brain barrier. Low values of charge density storage (<0.3 µC/mm2) are suggested; that is, electrodes are generally surface electrodes. For nerve stimulation circular (ring) electrodes are placed within an insulating cuff; consequently, smaller amounts of current are required because the field is greatly confined. Also lower current tends to minimize unwanted excitation of surrounding tissue. Finally, intramuscular electrodes, because of the flexing that must be withstood, are usually of the coiled-wire variety discussed above.
In the stimulation of the brain, of particular concern is preventing breakdown of the blood-brain barrier. Low values of charge density storage (<0.3 µC/mm2) are suggested; that is, electrodes are generally surface electrodes. For nerve stimulation circular (ring) electrodes are placed within an insulating cuff; consequently, smaller amounts of current are required because the field is greatly confined. Also lower current tends to minimize unwanted excitation of surrounding tissue. Finally, intramuscular electrodes, because of the flexing that must be withstood, are usually of the coiled-wire variety discussed above.
REFERENCES
REFERENCES, BOOKS


